The Operational Monad Tutorial

In this tutorial, I would like to present monads from the viewpoint of operational semantics and how it makes designing and implementing new monads a piece of cake. Examples include a monad for random number generation and a breadth-first implementation of monadic parser combinators.

This article was first published in issue 15 of The Monad.Reader.

Introduction

Another monad tutorial? Oh my god, why!? Fear not, this article is aimed at Haskellers who are already familiar with monads, though I have of course tried to keep the material as accessible as possible; the first two sections may serve as an initial introduction to monads and the monad laws for the brave.

In this tutorial, I would like to present monads from the viewpoint of operational semantics and how it makes designing and implementing new monads a piece of cake. Put differently, s -> (a,s) is not the only way to implement the state monad and this tutorial aims to present a much more systematic way. I think it is still regrettably underused, hence this text.

The main idea is to view monads as a sequence of instructions to be executed by a machine, so that the task of implementing monads is equivalent to writing an interpreter. The introductory example will be a stack automaton, followed by a remark on a monad for random numbers. Then, to showcase the simplicity of this approach, we will implement backtracking parser combinators, culminating in a straightforward breadth-first implementation equivalent to Claessen’s parallel parsing processes.

For those in the know, I’m basically going to present the principles of Chuan-kai Lin’s Unimo paper. The approach is neither new nor unfamiliar; for example, John Hughes already used it to derive the state monad. But until I read Lin’s paper, I did not understand how valuable it is when done systematically and in Haskell. Ryan Ingram’s MonadPrompt package is another recent formulation.

To encourage reuse, I have also released a package operational on hackage which collects the generic bits of these ideas in a small library. For convenient study, the source code from each section of this article is also available.

Stack Machine - List of Instructions?

Our introductory example will be a stack machine, i.e. an imperative mini-language featuring two instructions push and pop for pushing and popping values onto and from a stack.

In other words, I have imperative programs like the following in mind:

push 5; push 42; pop;

Instructions are separated by semicolons. As shown in the following picture, this program first puts the number 5 on the stack, then puts the number 42 on top of the stack and proceeds to remove it again.

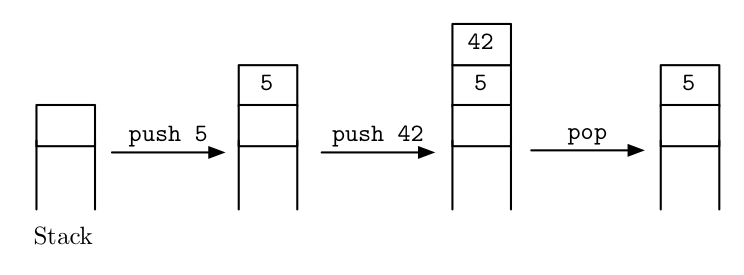
Example stack program

How can we embed such programs into Haskell?

Representation

First we need some way of representing the program text, for instance as a list of instructions:

type Program instr    = [instr]
type StackProgram     = Program StackInstruction
data StackInstruction = Push Int | Pop

Our example is represented as

example = Push 5 : Push 42 : Pop : []

In a sense, the colon (:) for building lists takes the role of the semicolon for sequencing instructions.

Concatenation and thoughts on the interface

Note that this representation gives us a very convenient tool for assembling bigger programs from smaller subprograms: list concatenation (++). For instance,

exampleTwice = example ++ example
    = Push 5 : Push 42 : Pop : Push 5 : Push 42 : Pop : []

is a program that executes example twice. Together with the empty program

empty = []

concatenation obeys the following three well-known laws:

 empty ++ is      =  is                  -- left unit
    is ++ empty   =  is                  -- right unit
(is ++ js) ++ ks  =  is ++ (js ++ ks)    -- associativity

which seem almost too evident to be worth mentioning. For example, it is customary to leave out the parenthesis in the last line altogether.

Once accustomed to the notion of programs and (++) to combine them, the special case of single instructions and (:) for sequencing them is unnecessary. The user of our language does not care that we deem push and pop to be primitive operations but not, for example, the program

replace a = Pop : Push a : []

which replaces the topmost stack element with a; he is entirely content to be given two programs

push :: Int -> StackProgram
pop  :: StackProgram

and two general combinators for building new ones

empty :: StackProgram
(++)  :: StackProgram -> StackProgram -> StackProgram

without any mention of the distinction between single instruction and compound program. Their difference is but an implementation detail.

Interpreter

Well, to be entirely content, the user also needs a way to run programs. In particular, we need to implement a function interpret that maps the program text to its intended meaning, here a function that transforms a stack of integers.

type Stack a = [a]

interpret :: StackProgram -> (Stack Int -> Stack Int)

The implementation follows the style of operational semantics: inspect the first instruction, change the stack accordingly, and recursively proceed with the remaining list of instructions is:

interpret (Push a : is) stack = interpret is (a : stack)
interpret (Pop    : is) stack = interpret is (tail stack)
interpret []            stack = stack

Oops

“All well and good, but why all the fuss with ‘monads’ then, when lists of instructions will do?” you may ask. Alas, the problem is of course that lists won’t do! We forgot something very important: our programs are completely unable to inspect values from the stack.

For instance, how to write a program that pops the two topmost values and pushes their sum onto the stack? Clearly, we want something like

a <- pop;
b <- pop;
push (a+b);

where each pop returns the element just removed and the arrow <- binds it to a variable. But binding variables is simply impossible to express with our current representation of programs as lists of instructions.

Stack Machine - Monad

Well, if ordinary lists of instructions are not enough to represent programs that involve binding variables like

a <- pop; b <- pop; push (a+b);

then let’s invent some fancy kind of list of instructions that will! The following presentation will be in close analogy to the structure of the previous section.

Representation

Return types

First, if we want to interpret pop as a function that returns something, we had better label it with the type of the value returned! Hence, instead of a plain type

Pop :: StackInstruction

we need an additional type argument

Pop :: StackInstruction Int

which indicates that the Pop instruction somehow returns a value of type Int.

For simplicity, we attribute a return type to push as well, even though it doesn’t really return anything. This can modeled just fine with the unit type ().

Push 42 :: StackInstruction ()
Push    :: Int -> StackInstruction ()

Putting both together, our type of instructions will become

data StackInstruction a where
    Pop  :: StackInstruction Int
    Push :: Int -> StackInstruction ()

If this syntax is alien to you: this is a Generalized Algebraic Data Type (GADT) which allows us to define a data type by declaring the types of its constructors directly. As of Haskell 2010, GADTs are not yet part of the language standard, but they are supported by GHC.

Like instructions, we also have to annotate programs with their return type, so that the definition for StackProgram becomes

data Program instr a where ...

type StackProgram a = Program StackInstruction a

As before, instr is the type of instructions, whereas a is the newly annotated return type.

Binding variables

How to represent the binding of variables? Lambda abstractions will do the trick; imagine the following:

take a binding a <- pop; rest
turn the arrow to the right pop -> a; rest
and use a lambda expression to move it past the semicolon pop; \a -> rest

Voila, the last step can be represented in Haskell, with a constructor named Then taking the role of the semicolon:

Pop `Then` \a -> rest

The idea is that Then plugs the value returned by pop into the variable a. By the way, this is akin to how let expressions can be expressed as lambda abstractions in Haskell:

let a = foo in bar   <=>   (\a -> bar) foo

Anyway, our motivating example can now be represented as

example2 = Pop `Then` (\a -> Pop `Then`
                        (\b -> Push (a+b) `Then` Return))

where Return represents the empty program which we will discuss in a moment. Remember that parentheses around the lambda expressions are optional, so we can also write

example2 = Pop `Then` \a ->
           Pop `Then` \b ->
           Push (a+b) `Then`
           Return

It is instructive to think about the type of Then. It has to be

Then :: instr a -> (a -> Program instr b) -> Program instr b

Except for the return type a in instr a and the lambda abstraction, this is entirely analogous to the “cons” operation (:) for lists.

Empty program

The empty program, corresponding to the empty list [], is best represented by a constructor

Return :: a -> Program instr a

that is not “entirely empty” but rather denotes a trivial instruction that just returns the given value a (hence the name). This is very useful, since we can now choose return values freely. For instance,

example3 = Pop `Then` \a -> Pop `Then` \b -> Return (a*b)

is a program that pops two values from the stack but whose return value is their product.

The fancy list

Taking everything together, we obtain a fancy list of instructions, once again a GADT:

data Program instr a where
    Then   :: instr a -> (a -> Program instr b) -> Program instr b
    Return :: a -> Program instr a

And specialized to our stack machine language, we get

type StackProgram a = Program StackInstruction a

Interpreter

Before thinking thinking further about our new representation, let’s first write the interpreter to see the stack machine in action. This time, however, we are not interested in the final stack, only in the value returned.

interpret :: StackProgram a -> (Stack Int -> a)
interpret (Push a `Then` is) stack     = interpret (is ()) (a:stack)
interpret (Pop    `Then` is) (b:stack) = interpret (is b ) stack
interpret (Return c)         stack     = c

The implementation is like the previous one, except that now, we also have to pass the return values like () and b to the remaining instructions is.

Our example program executes as expected:

GHCi> interpret example3 [7,11]
77

Concatenation and interface

Just as with lists, we can build large programs by concatenating smaller subprograms. And as before, we don’t want the user to bother with the distinction between single instruction and compound program.

We begin with the latter: the function

singleton :: instr a -> Program instr a
singleton i = i `Then` Return

takes the role of \x -> [x] and helps us blur the line between program and instructions:

pop  :: StackProgram Int
push :: Int -> StackProgram ()

pop  = singleton Pop
push = singleton . Push

Now, we define the concatenation operator (often dubbed “bind”) that glues two programs together:

(>>=) :: Program i a -> (a -> Program i b) -> Program i b
(Return a)    >>= js  = js a
(i `Then` is) >>= js  = i `Then` (\a -> is a >>= js)

Apart from the new symbol (>>=) and the new type signature, the purpose and implementation is entirely analogous to (++). And as before, together with the empty program,

return = Return

it obeys three evident laws

return a >>= is     = is a                        -- left unit
is >>= return       = is                          -- right unit
(is >>= js) >>= ks  = is >>= (\a -> js a >>= ks)  -- associativity

also called the monad laws. Since we need to pass return values, the laws are slightly different from the concatenation laws for ordinary lists, but their essence is the same.

The reason that these equations are called the “monad laws” is that any data type supporting two such operations and obeying the three laws is called a monad. In Haskell, monads are assembled in the type class Monad, so we’d have to make an instance

instance Monad (Program instr) where
    (>>=)  = ...
    return = ...

This is similar to lists which are said to constitute a monoid.

We conclude the first part of this tutorial by remarking that the (>>=) operator is the basis for many other functions that build big programs from small ones; these can be found in the Control.Monad module and are described elsewhere.

What we’ve done so far

Those familiar with the state monad will recognize that the whole stack machine was just

State (Stack Int)

in disguise. But surprisingly, we haven’t used the pattern s -> (a,s) for threading state anywhere! Instead, we were able to implement the equivalent of

evalState :: State s -> (s -> a)

directly, even though the type s -> a by itself is too “weak” to serve as an implementation of the state monad.

This is a very general phenomenon and it is of course the main benefit of the operational viewpoint and the new Program instr a type. No matter what we choose as interpreter function or instruction set, the monad laws for (>>=) and return will always hold, for they are entirely independent of these choices. This makes it much easier to define and implement new monads and the remainder of this article aims to give a taste of its power.

Multiple Interpreters

A first advantage of the operational approach is that it allows us to equip one and the same monad with multiple interpreters. We’ll demonstrate this flexibility with an example monad Random that expresses randomness and probability distributions.

The ability to write multiple interpreters is also very useful for implementing games, specifically to account for both human and computer opponents as well as replaying a game from a script. This is what prompted Ryan Ingram to write his MonadPrompt package.

Random Numbers

At the heart of random computations is a type Random a which denotes random variables taking values in a. Traditionally, the type a would be a numeric type like Int, so that Random Int denotes “random numbers”. But for the Haskell programmer, it is only natural to generalize it to any type a. This generalization is also very useful, because it reveals hidden structure: it turns out that Random is actually a monad.

There are two ways to implement this monad: one way is to interpret random variables as a recipe for creating pseudo-random values from a seed, which is commonly written

type Random a = StdGen -> (a,StdGen)

The other is to view them as a probability distribution, as for example expressed in probabilistic functional programming as

type Probability = Double
type Random a    = [(a,Probability)]

Traditionally, we’d have to choose between one way or the other depending on the application. But with the operational approach, we can have our cake and eat it, too! The two ways of implementing random variables can be delegated to two different interpreter functions for one and the same monad Random.

For demonstration purposes, we represent Random as a language with just one instruction uniform that randomly selects an element from a list with uniform probability

type Random a = Program RandomInstruction a

data RandomInstruction a where
    Uniform :: [a] -> RandomInstruction a

uniform :: [a] -> Random a
uniform = singleton . Uniform

For example, a roll of a die is modeled as

die :: Random Int
die = uniform [1..6]

and the sum of two dice rolls is

sum2Dies = die >>= \a -> die >>= \b -> return (a+b)

Now, the two different interpretations are: sampling a random variable by generating pseudo-random values

sample :: Random a -> StdGen -> (a,StdGen)
sample (Return a)             gen = (a,gen)
sample (Uniform xs `Then` is) gen = sample (is $ xs !! k) gen'
    where (k,gen') = System.Random.randomR (0,length xs-1) gen

and calculating its probability distribution

distribution :: Random a -> [(a,Probability)]
distribution (Return a)             = [(a,1)]
distribution (Uniform xs `Then` is) =
    [(a,p/n) | x <- xs, (a,p) <- distribution (is x)]
    where n = fromIntegral (length xs)

Truth to be told, the distribution interpreter has a flaw, namely that it never tallies the probabilities of equal outcomes. That’s because this would require an additional Eq a constraint on the types of return and (>>=), which is unfortunately not possible with the current Monad type class. A workaround for this known limitation can be found in the norm function from the paper on probabilistic functional programming.

Monadic Parser Combinators

Now, it is time to demonstrate that the operational viewpoint also makes the implementation of otherwise advanced monads a piece of cake. Our example will be monadic parser combinators and for the remainder of this article, I will assume that you are somewhat familiar with them already. The goal will be to derive an implementation of Koen Claessen’s ideas from scratch.

Primitives

At their core, monadic parser combinators are a monad Parser with just three primitives:

symbol :: Parser Char
mzero  :: Parser a
mplus  :: Parser a -> Parser a -> Parser a

which represent

respectively. (The last two operations define the MonadPlus type class.) Furthermore, we need an interpreter, i.e. a function

interpret :: Parser a -> (String -> [a])

that runs the parser on the string and returns all successful parses.

The three primitives are enough to express virtually any parsing problem; here is an example of a parser number that recognizes integers:

satisfies p = symbol >>= \c -> if p c then return c else mzero 
many  p     = return [] `mplus` many1 p
many1 p     = liftM2 (:) p (many p) 
digit       = satisfies isDigit >>= \c -> return (ord c - ord '0')
number      = many1 digit >>= return . foldl (\x d -> 10*x + d) 0

A first implementation

The instruction set for our parser language will of course consist of these three primitive operations:

data ParserInstruction a where
    Symbol :: ParserInstruction Char
    MZero  :: ParserInstruction a
    MPlus  :: Parser a -> Parser a -> ParserInstruction a

type Parser a = Program ParserInstruction a

A straightforward implementation of interpret looks like this:

interpret :: Parser a -> String -> [a]
interpret (Return a)            s = if null s then [a] else []
interpret (Symbol    `Then` is) s = case s of
    c:cs -> interpret (is c) cs
    []   -> []
interpret (MZero     `Then` is) s = []
interpret (MPlus p q `Then` is) s =
    interpret (p >>= is) s ++ interpret (q >>= is) s

For each instruction, we specify the intended effects, often calling interpret recursively on the remaining program is. In prose, the four cases are

A note on technique

The cases for MZero and MPlus are a bit roundabout; the equations

interpret mzero       = \s -> []
interpret (mplus p q) = \s -> interpret p s ++ interpret q s

express our intention more plainly. Of course, these two equations do not constitute valid Haskell code for we may not pattern match on mzero or mplus directly. The only thing we may pattern match on is a constructor, for example like this

interpret (Mplus p q `Then` is) = ...

But even though our final Haskell code will have this form, this does not mean that jotting down the left hand side and thinking hard about the ... is the best way to write Haskell code. No, we should rather use the full power of purely functional programming and use a more calculational approach, deriving the pattern matches from more evident equations like the ones above.

In this case, we can combine the two equations with the MonadPlus laws

    mzero >>= m = mzero
mplus p q >>= m = mplus (p >>= m) (q >>= m)

which specify how mzero and mplus interact with (>>=), to derive the desired pattern match

  interpret (Mplus p q `Then` is)
=   { definition of concatenation and mplus }
  interpret (mplus p q >>= is)
=   { MonadPlus law }
  interpret (mplus (p >>= is) (q >>= is))
=   { intended meaning }
  \s -> interpret (p >>= is) s ++ interpret (q >>= is) s

Now, in light of the first step of this derivation, I even suggest to forget about constructors entirely and instead regard

interpret (mplus p q >>= is) = ...

as “valid” Haskell code; after all, it is straightforwardly converted to a valid pattern match. In other words, it is once again beneficial to not distinguish between single instructions and compound programs, at least in notation.

Depth-first

Unfortunately, our first implementation has a potential space leak, namely in the case

interpret (MPlus p q `Then` is) s =
    interpret (p >>= is) s ++ interpret (q >>= is) s

The string s is shared by the recursive calls and has to be held in memory for a long time.

In particular, the implementation will try to parse s with the parser p >>= is first, and then backtrack to the beginning of s to parse it again with the second alternative q >>= is. That’s why this is called a depth-first or backtracking implementation. The string s has to be held in memory as long the second parser has not started yet.

Breadth-first

To ameliorate the space leak, we would like to create a breadth-first implementation, one which does not try alternative parsers in sequence, but rather keeps a collection of all possible alternatives and advances them at once.

How to make this precise? The key idea is the following equation:

  (symbol >>= is) `mplus` (symbol >>= js)
=  symbol >>= (\c -> is c `mplus` js c)

When the parsers on both sides of mplus are waiting for the next input symbol, we can group them together and make sure that the next symbol will be fetched only once from the input stream.

Clearly, this equation readily extends to more than two parsers, like for example

  (symbol >>= is) `mplus` (symbol >>= js) `mplus` (symbol >>= ks)
=  symbol >>= (\c -> is c `mplus` js c `mplus` ks c)

and so on.

We want to use this equation as a function definition, mapping the left hand side to the right hand side. Of course, we can’t do so directly because the left hand side is not one of the four patterns we can match upon. But thanks to the MonadPlus laws, what we can do is to rewrite any parser into this form, namely with a function

expand :: Parser a -> [Parser a]
expand (MPlus p q `Then` is) = expand (p >>= is) ++
                               expand (q >>= is)
expand (MZero     `Then` is) = []
expand x                     = [x]

The idea is that expand fulfills

foldr mplus mzero . expand = id

and thus turns a parser into a list of summands which we now can pattern match upon. In other words, this function expands parsers matching mzero >>= is and mplus p q >>= is until only summands of the form symbol >>= is and return a remain.

With the parser expressed as a big “sum”, we can now apply our key idea and group all summands of the form symbol >>= is; and we also have to take care of the other summands of the form return a. The following definition will do the right thing:

interpret :: Parser a -> String -> [a]
interpret p = interpret' (expand p)
    where
    interpret' :: [Parser a] -> String -> [a]
    interpret' ps []     = [a | Return a <- ps]
    interpret' ps (c:cs) = interpret'
        [p | (Symbol `Then` is) <- ps, p <- expand (is c)] cs

Namely, how to handle each of the summands depends on the input stream:

That’s it, this is our breadth-first interpreter, obtained by using laws and equations to rewrite instruction lists. It is equivalent to Koen Claessen’s implementation.

As an amusing last remark, I would like to mention that our calculations can be visualized as high school algebra if we ignore that (>>=) has to pass around variables, as shown in the following table:

Term Mathematical operation
return 1
(>>=) × multiplication
mzero 0
mplus + addition
symbol x indeterminate

For example, our key idea corresponds to the distributive law

x × a + x × b = x × (a + b)

and the monad and MonadPlus laws have well-known counterparts in algebra as well.

Conclusion

Further Examples

I hope I have managed to convincingly demonstrate the virtues of the operational viewpoint with my choice of examples.

There are many other advanced monads whose implementations also become clearer when approached this way, such as the list monad transformer (where the naive m [a] is known not to work), Oleg Kiselyov’s LogicT, Koen Claessen’s poor man’s concurrency monad, as well coroutines like Peter Thiemann’s ingenious WASH which includes a monad for tracking session state in a web server.

The operational package includes a few of these examples.

Connection with the Continuation Monad

Traditionally, the continuation monad transformer

data Cont m a = Cont { runCont :: forall b. (a -> m b) -> m b }

has been used to implement these advanced monads. This is no accident; both approaches are capable of implementing any monad. In fact, they are almost the same thing: the continuation monad is the refunctionalization of instructions as functions

\k -> interpret (Instruction `Then` k)

But alas, I think that this unfortunate melange of instruction, interpreter and continuation does not explain or clarify what is going on; it is the algebraic data type Program that offers a clear notion of what a monad is and what it means to implement one. Hence, in my opinion, the algebraic data type should be the preferred way of presenting new monads and also of implementing them, at least before program optimizations.

Actually, Program is not a plain algebraic data type, it is a generalized algebraic data type. It seems to me that this is also the reason why the continuation monad has found more use, despite being conceptually more difficult: GADTs simply weren’t available in Haskell. I believe that the Program type is a strong argument to include GADTs into a future Haskell standard.

Drawbacks

Compared to specialized implementations, like for example s -> (a,s) for the state monad, the operational approach is not entirely without drawbacks.

First, the given implementation of (>>=) has the same quadratic running time problem as (++) when used in a left-associative fashion. Fortunately, this can be ameliorated with a different (fancy) list data type; the operational library implements one.

Second, and this cannot be ameliorated, we lose laziness. The state monad represented as s -> (a,s) can cope with some infinite programs like

evalState (sequence . repeat . state $ \s -> (s,s+1)) 0

whereas the list of instructions approach has no hope of ever handling that, since only the very last Return instruction can return values.

I also think that this loss of laziness also makes value recursion a la MonadFix very difficult.

About the author

After some initial programming experience in Pascal, Heinrich Apfelmus picked up Haskell and purely functional programming just at the dawn of the new millenium. He has never looked back ever since, for he not only admires Haskell’s mathematical elegance, but also its practicality in personal life. For instance, he was always too lazy to tie knots, but that has changed and he now accepts shoe laces instead of velcro.

Comments

Some HTML formatting is allowed.