Fun with Morse Code

Wanted: a short and clever morse code decoder in Haskell. This article presents a series of successively smaller solutions that gradually include computer science concepts like dichotomic search, stack-based languages and finally deforestation, an optimization technique specific to purely functional languages like Haskell.

Table of contents

Introduction
A simple first solution
Dichotomic search
Reverse Polish Notation
Deforestation
- Chopping trees
- A chainsaw called ‘catamorphism’
  - Derivation
  - General pattern
Where to go from here

This article previously appeared in issue 14 of The Monad.Reader.

Introduction

In a post to reddit, user CharlieDancey presented a challenge to write a short and clever morse code decoder. Of course, what could be more clever than writing it in Haskell? ;-)

In the following, I’ll present a series of solutions that gradually include dichotomic search (the straightforward generalization of binary search), stack-based languages or reverse polish notation, and finally deforestation (also called fusion), an optimization technique specific to purely functional languages like Haskell.

For your convenience, source code for the individual sections is available.

A simple first solution

Morse code was designed to be produced and read, or rather heard by humans, who have to memorize the following table:

To write a program that decodes sequences of dots and dashes like

-- --- .-. ... .    -.-. --- -.. .

into letters, we will have to store this table in some form. For instance, we could store each letter and corresponding morse code in a big association list

type MorseCode = String

dict :: [(MorseCode, Char)]
dict =
    [(".-"   , 'A'),
     ("-..." , 'B'),
     ("-.-." , 'C'),
     ...

which we name dict because it’s a dictionary translating between the latin alphabet and morse code. To decode a letter, we simply browse through this list to determine whether it contains a given code of dots and dashes

decodeLetter :: MorseCode -> Char
decodeLetter code = maybe ' ' id $ lookup code dict

Decoding a whole sequence of letters is done with

decode = map decodeLetter . words

so that we have for example

> decode "-- --- .-. ...    . -.-. --- -.. ."
"MORSECODE"

Of course, association lists are a rather slow data structure. A binary search tree, trie, or hash table would be a better choice. But fortunately, it is very easy to change data structures in Haskell. All you have to do is to a qualified import of a different module, such as Data.Map, and change the definition of dict to

dict :: Data.Map.Map MorseCode Char
dict = Data.Map.fromList $
    [(".-"   , 'A'),
     ("-..." , 'B'),
     ("-.-." , 'C'),
     ...

and use Data.Map.lookup instead of Data.List.lookup.

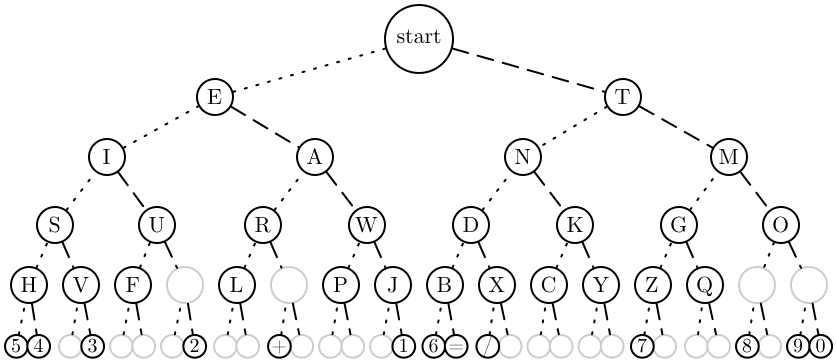
Dichotomic search

Faithfully replicating the morse code table is clear and preferable, but makes for quite large source code. So, let’s make an exception today and think of something as clever as we can.

The idea is the following: whenever an encoded letter starts with a dash '-', we know that it can’t be for example an A or E, because those start with a dot '.'. And if the next symbol is a dot, then it can’t be a G or M because their second symbol is a dash. With each symbol we read, more and more alternatives disappear until we are left with a single alternative. We can depict this with a binary tree:

At each node, the left subtree contains all the letters that can be obtained by adding a dot to the current letter, while the right subtree contains those letters that can be obtained with a dash. This is illustrated by means of a dotted line connected to the left subtree and a dashed line connected to the right subtree.

Now, to decode a letter, we simply start at the root of the tree and follow the dotted or dashed lines depending on the symbols read. For instance, to decode the sequence "-...", we have to go right once and then left thrice, ending up at the letter B. This procedure is also called dichotomic search because at each point in our search for the right letter, we ask a yes/no question “Dot or dash?” (a dichotomy) that partitions the remaining search space into to disjoint parts.

Let’s implement this in Haskell. First, we assume that our dictionary is given as a tree

data Tree a = Leaf
            | Branch { tag   :: a
                     , left  :: Tree a
                     , right :: Tree a }

dict :: Tree Char
dict = Branch ' ' (Branch 'E' ... ) (Branch 'T' ...)

Of course, writing out the dict tree in full is going to be repetitive and boring, but let’s just imagine we have already done that. Then, decoding a letter by walking down the tree is simply a left fold over the code word

decodeLetter = tag . foldl (flip step) dict
    where
    step '.' = left
    step '-' = right

In this case, the accumulated value of the fold is the current subtree, although the term “accumulate” is a bit misleading in that we don’t make the dictionary bigger; we make it smaller by passing to a subtree.

The curious reader may notice that we have actually implemented a trie.

Reverse Polish Notation

Now, let’s reduce the source code needed for the dictionary tree. In Haskell, we’d have to write something like

dict = Branch ' ' (Branch 'E' ... ) (Branch 'T' ...)

Compared to the association list, we got rid of the dots '.' and dashes '-', they have been made implicit in the structure of our tree. But we still need a lot of parenthesis and applications of the Branch function.

A clever way to get rid of parenthesis is reverse polish notation, commonly used in stack-based languages. The idea is that a program in such a language is a sequence of instructions that pop and push values from a stack. For example,

1 2 +

is a program to calculate 1 plus 2. Reading from left to right, the first instruction is 1 which pushes the integer 1 onto the stack. The second instruction is 2, pushing 2 onto the stack. And finally, the instruction + pops the two topmost integers from the stack and pushes their sum onto the stack. This procedure is visualized as follows:

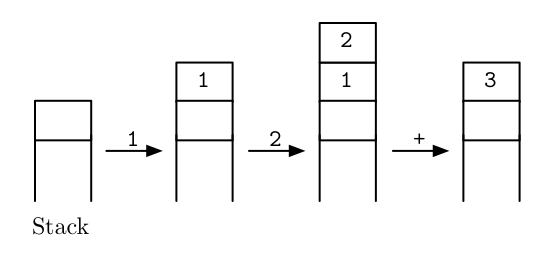
Execution of the stack-based program 1 2 +

To see how that eliminates the need for parenthesis, take a look the program

1 2 + 3 4 + +

which calculates the sum (1+2)+(3+4).

To build our dictionary tree, we are going to devise a very similar language. Instead of integers, the stack will store whole trees. In analogy to the numerals, there will be an instruction for pushing a Leaf onto the stack; and in analogy to +, there is going to be an instruction for applying the Branch constructor to the two topmost subtrees.

Here’s the program for building the tree, stored as a string:

program :: String
program = "__5__4H___3VS__F___2 UI__L__+_ R__P___1JWAE"
       ++ "__6__=B__/_XD__C__YKN__7_Z__QG__8_ __9__0 OMT "

Each character represents one instruction. The underscore '_' pushes a Leaf onto the stack while all the other character push a Branch tagged with the character in question onto the stack. The interpreter for this tiny programming language can be written using a simple left fold:

dict = interpret program
where
    interpret         = head . foldl exec []
    exec xs       '_' = Leaf         : xs    -- push Leaf
    exec (x:y:xs)  c  = Branch c y x : xs    -- combine subtrees

The stack xs is represented as a list of trees.

Deforestation

We have found a concise way to represent the morse code dictionary in source code, but cleverness does not end here. For instance, how about eliminating the tree entirely?

Chopping trees

Call graph

More precisely, it seems wasteful to construct the dictionary tree by creating leaves and connecting branches only to deconstruct them again when decoding letters. Wouldn’t it be more efficient to interpret the morse code tree as a call graph rather than as a data structure Tree Char?

In other words, imagine say a function e corresponding to the node labeled ‘E’ in the tree, and working as follows:

e :: MorseCode -> Char
e ('.':ds) = i ds
e ('-':ds) = a ds
e []       = 'E'

If the next symbol is a dot or dash, we proceed with the functions i or a corresponding to 'I' and 'A' respectively. And in case we have already reached the end of the code, we know that we have decoded an 'E'. The functions i and a work just like e, except that they proceed with other letters; and the morse code tree becomes their call graph.

A combinator…

Now, writing all these functions by hand would be most error-prone and tedious, they all look the same. But abstracting repetitive patterns is exactly where functional programming shines; we are to devise a combinator that automates the boring parts of the code for us.

What does this combinator look like? Well, the non-boring parts are the letter it represents and the two follow-up functions, so these will be parameters:

combinator :: Char                   -- letter
           -> (MorseCode -> Char)    -- function for dot
           -> (MorseCode -> Char)    -- function for dash
           -> (MorseCode -> Char)    -- result function

That’s all we need; we can implement

combinator c x y = \code -> case code of
    '.':ds -> x ds
    '-':ds -> y ds
    []     -> c

which allows us to write

e = combinator 'E' i a
i = combinator 'I' s u
... etc ...

…revealed!

But wait, what have we done? The type signature of combinator looks exactly like that of

Branch :: Char         -- letter
       -> Tree Char    -- tree for dot
       -> Tree Char    -- tree for dash
       -> Tree Char    -- result tree

but with the type Tree Char replaced by (MorseCode -> Char)! In fact, let’s rename the combinator to lowercase branch

branch c x y = \code -> case code of
    '.':ds -> x ds
    '-':ds -> y ds
    []     -> c

and observe that the tree of functions now reads

e = branch 'E' i a
i = branch 'I' s u
... etc ...

e = branch 'E' (branch 'I' ... ) (branch 'A' ...)

if we inline the function definitions. But this is of course just the tree from the section on dichotomic search with each Branch replaced by branch!

In other words, branch is like a drop-in replacement for the constructor Branch. To implement the morse code tree directly as functions instead of as an algebraic data type, we simply replace every occurrence of Branch with branch in our previous code. Thus, we have a new implementation

dict :: MorseCode -> Char
dict = interpret program
    where
    interpret         = head . foldl exec []
    exec xs       '_' = leaf         : xs    -- push leaf
    exec (x:y:xs)  c  = branch c y x : xs    -- combine subtrees

decodeLetter = dict

where

leaf = undefined

is a trivial replacement for the Leaf constructor.

A chainsaw called ‘catamorphism’

Derivation

To further understand how and why the replacement of Branch by branch works, it is instructive to derive it systematically from just the program text.

In particular, consider the implementation of decodeLetter from the earlier section on dichotomic search:

decodeLetter :: MorseCode -> Char
decodeLetter = tag . foldl (flip step) dict
    where
    step '.' = left
    step '-' = right

In this formulation, the focus is on the recursion over the input string performed by foldl, neglecting the recursive descent into the dictionary tree. Let’s systematically rewrite this code to highlight the latter.

First, we interpret it as converting the dictionary tree into a function that decodes letters

decodeLetter = decodeWith dict

decodeWith :: Tree Char -> (MorseCode -> Char)
decodeWith dict = tag . foldl (flip step) dict
    where
    step '.' = left
    step '-' = right

Then, we turn the foldl into explicit recursion

decodeWith dict []     = tag dict
decodeWith dict (d:ds) = decodeWith (step d dict) ds
    where
    step '.' = left
    step '-' = right

and dissolve the step function into the pattern matching

decodeWith dict []       = tag dict
decodeWith dict ('.':ds) = decodeWith (left  dict) ds
decodeWith dict ('-':ds) = decodeWith (right dict) ds

We group the pattern matching on the input code into a case expression

decodeWith dict = \code -> case code of
    []       -> tag dict
    ('.':ds) -> decodeWith (left  dict) ds
    ('-':ds) -> decodeWith (right dict) ds

and finally, we replace the field selectors by pattern matching on the tree, also noting the case of Leaf:

decodeWith Leaf           = undefined
decodeWith (Branch c x y) = \code -> case code of
    []       -> c
    ('.':ds) -> (decodeWith x) ds
    ('-':ds) -> (decodeWith y) ds

The recursion on the tree is apparent now, decodeWith simply traverses both subtrees and combines the results. We can make this even more evident by appealing to the combinator we defined in the previous section:

decodeWith Leaf           = leaf
decodeWith (Branch c x y) = branch c (decodeWith x) (decodeWith y)

In other words, decodeWith takes a tree and simply substitutes each Leaf constructor with leaf and each Branch constructor with branch.

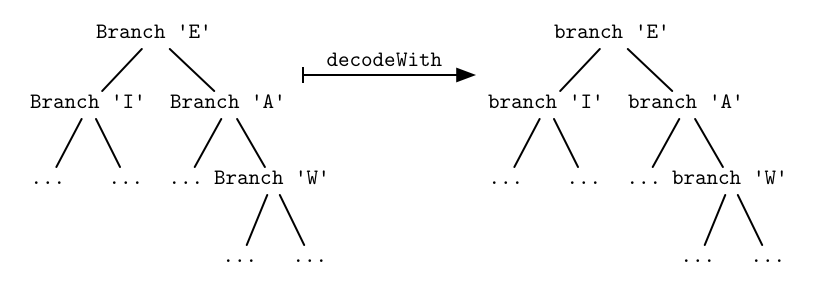
Substituting constructors Branch with functions branch

Of course, first using Branch and then replacing it with branch is a waste; we should rather use branch from the start and thus cut away the intermediate tree. That’s exactly what we’ve done in the previous section!

General pattern

Replacing constructors is a very general pattern, not restricted to binary trees. For instance, you probably know following function:

foldr f z []     = z
foldr f z (x:xs) = x `f` foldr f z xs

It’s the good old fold! And at its heart, it just replaces the constructors of the list data type: z is the substitute for the empty list [], and f is put in lieu of the (:) constructor.

In its honor, any function that substitutes constructors in such fashion is known as a generalized fold. A more exotic but commonly used alternative name is “catamorphism”. In other words, decodeWith is a catamorphism.

In this generality, the idea of deforestation is that instead of first constructing a data structure and then chopping it up with a catamorphism, it is more efficient to saw the pieces properly at the time of creation. For example, creating a list and then adding all elements

sum [1..100] = foldr (+) 0 (enumFromTo 1 100)

is less efficient than adding the elements as they are created

sumFromTo a b                            -- changes to enumFromTo
    | a > b     = 0                      -- 0 replaces []
    | otherwise = a + sumFromTo (a+1) b  -- + replaces (:)

Merging two functions in this fashion is also called fusion.

Performing deforestation manually, as we did, sacrifices reusability: the morse code tree only exists as a call graph and cannot be printed out anymore, and sumFromTo is not nearly as useful as are sum and enumFromTo were.

Hence, the goal is to teach the compiler to automatically fuse catamorphisms with their structure creating counterparts, the so called anamorphisms. That’s what efforts like a short-cut to deforestation and the recent stream fusion are set out to do, yielding dramatic gains in efficiency while preserving the compositional style.

Where to go from here

I hope you had fun doodling around with morse code; I certainly did. If you long for more, here a few suggestions:

Cutting words

While we’re at it, the intermediate lists created by words in

decode = map decodeLetter . words

can be deforested as well and fused into the letter decoding. Try it yourself, or see the example source code.

Polish notation and parsing

Polish notation, the converse of reverse polish notation, puts function symbols before their arguments and is thus closer to the Haskell syntax. When the arities of the functions are known in advance, like 2 for Branch and 0 for Leaf, this notation doesn’t require parenthesis either. Write a program in polish notation and a corresponding tiny interpreter to create the morse code tree.

Comparing to C

Since deforestation is supposed to make things faster, how about comparing our deforested morse code tree to say an implementation in C? But instead of doing benchmarks, let me give two general remarks on the machine representation.

First, one might think that the call graph we’ve built is compiled to function calls, with e calling i or a and each function having different machine code, just as we originally intended. But this is actually not the case. When defined with branch, the functions are represented as closures, sharing the same machine code but carrying different records that store their free variables c, x and y. This is not very different from storing c, x and y in a Branch constructor. Template Haskell or some kind of partial evaluation would be needed to hard-code the free variables into the executable. For more on the Haskell execution model, take a look at the GHC commentary.

Second, all our implementations decipher a letter by follow a chain of pointers: descending a tree means following pointers to deeper nodes, and making procedure calls means repeatedly jumping to different code parts. This of course raises questions of cache locality, branch prediction or memory requirements for storing all these pointers.

In C, however, there is another technique available: instead of following a chain of pointers to get to the destination, the address of the final stop is calculated directly with pointer arithmetic. The following example illustrates this:

#include <stdio.h>
#include <string.h>
char buf[99], tree[] = " ETIANMSURWDKGOHVF L PJBXCYZQ  ";
int main() {
    while (scanf("%s", buf)) {
        int n, t=0;
        for(n=0; buf[n]!=0; n++)
            t = 2*t + 1 + (buf[n]&1); /* compute destination */
        putchar(tree[t]);             /* fetch letter */
    }
}

Here, the tree is represented as an array and paths to nodes are encoded as (zero-less) binary numbers. The program calculates the path t to the proper letter and then fetches it with an O(1) memory lookup. Compare also the morse code translator by reddit user kayamon.

Since the number of memory accesses is kept to a minimum, this technique is the most efficient; but it is impossible to reproduce with algebraic data types alone. Fortunately, arrays libraries are readily available in Haskell as well.

The main drawback of this approach, and of arrays in general, is the lack of clarity; indices are notorious for being non-descript and messy. The raw index arithmetic in the example C code above sure seems like magic!

Such magic is best hidden behind a descriptive abstract data type. How about rewriting the example in Haskell such that decodeLetter looks exactly like the one in the section on dichotomic search? In other words, the abstract data type is to support the functions left, right and tag. One possible solution can be found in the source code accompanying this article.