Crypto me a tea

Introduction to FRP - Why Applicative Functors?

This post is for novice Haskell programmers and answers the question “What is FRP and why do FRP libraries require me to learn about applicative functors?”. It will be added to the documentation of the reactive-banana library, eventually.

EDIT: Changed wording slightly in response to comments.

Introduction to FRP - Why Applicative Functors?

Many if not all FRP (Functional Reactive Programming) libraries, reactive-banana included, export an API that is based on functors, applicative functors or other higher-kinded types like arrows. This section explains why that is and what it means for the novice Haskell programmer.

The idea of time-varying values

The two main data types of the reactive-banana library are behaviors and events. The type constructor Behavior represents a time-varying value, i.e. you can think of it as a function

type Behavior a = Time -> a

On the other hand, the type constructor Event represents a sequence of event occurrences. Think of it as a list

type Event a = [(Time,a)]

Pictorially, you could represent them like this: a behavior traces the evolution of a value over time

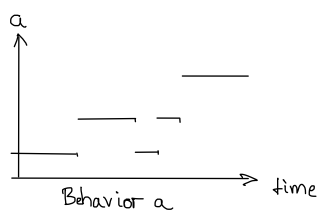
while an event consists of several, possibly simultaneous event occurrences.

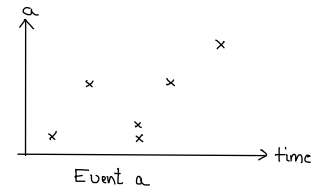
The promise of functional reactive programming is that these two notions allow you to code interactive programs like animations, graphical user interfaces (GUI) and so on much more easily and declaratively than previously possible. Indeed, representing, say, the position of a player character on the screen as a function of time is a remarkable and powerful idea. Of course, you can only fathom this idea if you are used to programming languages with first-class functions.

Now, you could just take these two type definitions above and use them to code animations to your heart’s content; after all, they are legal Haskell code. This is pretty much what Conal Elliott and Paul Hudak did in their seminal paper “Functional Reactive Animation”. Unfortunately, the computational costs of this approach are prohibitive. While trading clock cycles for expressivity is often worth it, the costs here are much more than a constant factor. A direct implementation is simply not practical.

Abstraction and combinators

The solution to the problem above is, of course, abstraction. The FRP library gives us two data types Behavior and Event which behave very much like the definitions above. Internally, however, the library represents them very differently. But as long as these types behave as we desire, the difference is of no concern to us.

More precisely, the library not only gives us two types constructors Behavior and Event, but also a carefully chosen set of combinators (functions) for them. In reactive-banana version 0.2, the combinators are these:

filter  :: (a -> Bool) -> Event a -> Event a
accumE  :: a -> Event (a -> a) -> Event a
stepper :: a -> Event a -> Behavior a
apply   :: Behavior (a -> b) -> Event a -> Event b

instance Functor Event
instance Functor Behavior
instance Applicative Behavior
instance Monoid (Event a)

As you can see, some of the combinators are actually given by type class instances.

The deal with combinators is this: you may still think of Behavior as a function Time -> a, but you may no longer define a behavior directly, like b = \t -> 2*t. Instead, you may only use the combinators above to define new behaviors. This restriction to a certain set of functions is what guarantees an efficient implementation.

Some of these combinators, namely the type classes instances, belong to very general abstractions, like functor, applicative functor and monoid. They are applicable (pun intended) far beyond FRP, so understanding will pay off for other things as well. This is no surprise: every higher-kinded type, i.e. a type with a parameter, is simply very likely to belong to some of the abstractions here. Monads would be another common example, but it just so happens that they don’t show up in reactive-banana.

To learn more about applicative functors and the other type classes, have a look at Brent Yorgey’s Typeclassopedia. Understanding applicative functors is also very useful for understanding the apply combinator.

So much for the general philosophy behind every FRP library. The specific meaning and utility of the combinators in the reactive-banana library will be explained subsequently.

Comments