Crypto me a tea

FRP - Push-driven Implementations and Sharing

My reactive-banana library for functional reactive programming has changed considerably, though I’m not ready to release a new version just yet.

Namely, after some discussion with Conal Elliott, I have decided to implement a subset of his classic semantics, described in his paper Push-pull functional reactive programming. My main change to Conal’s semantics is to remove the switcher function and to not implement continuous behaviors.

The new semantics is a marked improvement over the previous state of my library, which did not have a well-defined semantics at all. While I think that Conal’s semantics are not the end-all – there are examples where it is less modular than one could hope for – it offers an excellent simplicity-to-power ratio. In particular, it allows for mutually recursive definitions that my previous version couldn’t handle. I think that if there’s a semantics that should serve as a reference point for every future FPR library, it’s this one.

I won’t describe Conal’s semantics here, however, that is left for a future post or future library documentation (but see here). Instead, I want to describe my path towards an efficient push-driven implementation, which was far trickier than I expected. One of the main problems was to reconcile sharing and union, that’s what I will write about here. The other problem I’m currently wrestling with is an implementation of accumE.

Setting up the Model

In Haskell, the first thing to do when you have a semantic model is to implement the simplest possible incarnation of it. This is what I did in the module Reactive.Banana.Model. While wholly inefficient, it has the definite advantage that it is likely correct.

Once you have an obviously correct implementation of the model, you can often derive an efficient one. Yes, that’s right, there are almost mechanical methods to obtain efficient implementations from hopelessly inefficient ones. If you don’t know about this already, I recomment to read functional pearls by Richard Bird, Graham Hutton and others. This is one of the key design methodologies for purely functional programming.

(You might think that this approach is unnecessary for simple problems; that there should be no harm in starting right with the efficient implementation because the problem is so simple. I have to admit that I followed this line of thought until recently, but I have changed my mind: there is harm in doing that. Namely, I have found that due to a lack of training, I’m unable to quickly find the most obviously correct implementation! Exercise: write a program that finds the sign of a permutation. If you start with a foldr or even primitive recursion, you have already missed the most obviously correct implementation.)

In my case, I haven’t been able to formally derive the push-driven implementation yet, mainly because of the issue of sharing which I will come to in a minute. Does anyone know how to derive programs with sharing?

Still, the model is very valuable, because I can now use QuickCheck to test whether my subsequent push-driven implementation is correct!

Pushing and Sharing

To keep the discussion simple, the basic object of consideration shall be a function

network :: Event A -> Event B -> Event C

that maps two input events to an output event. For instance, the input events might be mouse clicks and key presses while the output event some graphics that is drawn on the screen in response.

An example network is given by the following illustration, where e1 and e2 are input events while eout is the output event.

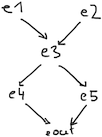
This corresponds to some code

eout, e1, e2, e3, e4, e5 :: Event Something
eout = union e4 e5
e4   = filter p e3
e5   = apply f e3
e3   = union e1 (filter q e2)

Imagine that the arrows are labeled with some fmap and filter; I have not bothered giving a more concrete example.

Now, the model implementation is inefficient because it is demand-driven, which means that evaluation starts at the output event and follows the arrows in reverse direction to calculate its occurences. Of course, if one of the arrows was a successful filter, this may have been a waste of time.

In contrast, a push-driven implementation starts at the input events and follows the arrows until the output event is reached. This has the advantage that evaluation aborts early if a filter decides to throw it away. So, a push-driven implementation would walk the following paths trought the network:

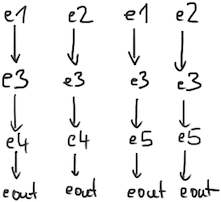
Unfortunately, this network would unnecessarily recaclulate the event e3. We have to pay attention to sharing; a proper version look like this:

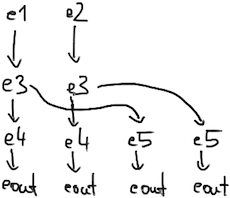
Note that the semantics of union force us to keep the order of paths intact; we cannot reorder paths to avoid the crossovers.

Observable Sharing

After some stupid ideas, I finally represented events as a standard abstract syntax tree. The main problem was to make sharing observable. After all, since Haskell is referentially transparent, you can’t normally distinguish between the shared variable e3 and its “copies”. I thought that using less syntax trees would make it easier to keep sharing, like in the model implementation, but that didn’t work out at all.

There are several known approaching to observable sharing in a syntax tree, but unfortunately, none of them applied straightforwardly because the situation here involves arbitrary types. A recent suggestion by Gill is to use the Typeable class, but then I would have to contrain all the combinators, like

union :: (Typeable a) => Event a -> Event a -> Event a
fmap  :: (Typeable a, Typeable b) => (a -> b) -> Event a -> Event b

which is an undue burden on user type signatures and disallows standard classes like Functor.

An older approach modeled after Claessen and Sands is to use unsafePerformIO to assign a unique number to every value, but there is no type-safe way to associate this number with data. Fortunately, it is possible to replace the number with an IORef to the associated data; that’s what I ended up doing. The price to pay is that the abstract syntax tree is now tied to my particular compilation scheme.

Incidentally, it would be possible to use the StableName a that Gill employs internally to the same effect if only they would support a generalized equality test

data Equal a b where
    Equal :: Equal a a

equal :: StableName a -> StableName b -> Maybe (Equal a b)

This allows you to wrap up existentially quantified versions of StableName into a list and extract them with the right type again later. So, if you happen to be a GHC hacker reading this, that would be something nice to have because I think it would allow me to dispense with unsafePerformIO.

Anyway, after being able to observe sharing, compiling union was fairly straightforward. Now, I’m wrestling with accumE.

Comments